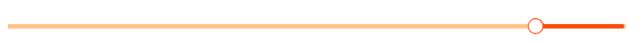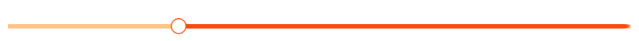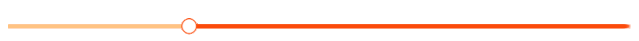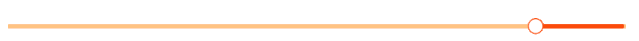解不等式

解法1：利用绝对值的定义

原不等式等价于（I）

或（II）

解（I）得

解（II）得

所以原不等式的解集为。

解法2：利用平方法

原不等式可化为两边平方得

解得

，所以原不等式的解集为。

解法3：利用绝对值的性质

原不等式等价于

即

解<1>得，或

解<2>得

所以原不等式的解集为。

解法4：零点分区间讨论

原不等式等价于

即等价于

或

或

解<1>得，解<2>得，<3>的解集是，所以原不等式的解集为。

解法5：图象法

原不等式等价于。

在直角坐标系中分别画及的图象。

由图可知，原不等式的解集为。

▍ 编辑：Wulibang（ID：2820092099）

▍ 来源：综合网络

▍ 声明：如有侵权，请联系删除；若需转载，请注明出处。